The Unusually Critical Implications of Math’s ‘Ham Sandwich Theorem’

Take into account lunch. Maybe a pleasant ham sandwich. A slice of a knife neatly halves the ham and its two bread slices. However what if you happen to slip? Oops, the ham now rests folded below a flipped plate, with one slice of bread on the ground and the opposite caught to the ceiling. Right here’s some solace: geometry ensures {that a} single straight lower, maybe utilizing a room-sized machete, can nonetheless completely bisect all three items of your tumbled lunch, leaving precisely half of the ham and half of every slice of bread on both aspect of the lower. That’s as a result of math’s “ham sandwich theorem” guarantees that for any three (doubtlessly uneven) objects in any orientation, there may be all the time some straight lower that concurrently bisects all of them. This truth has some weird implications in addition to some sobering ones because it pertains to gerrymandering in politics.

The theory generalizes to different dimensions as properly. A extra mathematical phrasing says that n objects in n-dimensional house could be concurrently bisected by an (n – 1)–dimensional lower. That ham sandwich is a little bit of a mouthful, however we’ll make it extra digestible. On a two-dimensional piece of paper, you may draw no matter two shapes you need, and there’ll all the time be a (one-dimensional) straight line that cuts each completely in half. To ensure an equal lower for 3 objects, we have to graduate to a few dimensions and lower them with a two-dimensional aircraft: consider that room-ravaging machete as slipping a skinny piece of paper between the 2 halves of the room. In three dimensions, the machete has three levels of freedom: you may scan it backwards and forwards throughout the room, then cease and rotate it to totally different angles, and then additionally rock the machete back and forth (like how carrots are sometimes lower obliquely, and never straight).

Should you can think about a four-dimensional ham sandwich, as mathematicians love to do, then you can additionally bisect a fourth ingredient with a three-dimensional lower.

On supporting science journalism

Should you’re having fun with this text, take into account supporting our award-winning journalism by subscribing. By buying a subscription you’re serving to to make sure the way forward for impactful tales in regards to the discoveries and concepts shaping our world immediately.

To get a taste for methods to show the ham sandwich theorem, take into account a simplified model: two shapes in two dimensions the place considered one of them is a circle and the opposite is a blob. Each line that passes by way of the middle of a circle bisects it (asymmetrical shapes don’t essentially have a middle like this; we’re utilizing a circle to make our lives simpler for now). How do we all know that considered one of these strains additionally bisects the blob? Choose a line by way of the middle of the circle that doesn’t intersect the blob in any respect. As depicted within the first panel under, 100% of the blob lies under the road. Now slowly rotate the road across the middle of the circle like a windmill. Finally, it breaches the blob, cuts by way of an increasing number of of it, after which passes under it the place zero % of the blob lies under the road. From this course of, we will deduce that there should be a second at which precisely 50 % of the blob lies under the road. We’re regularly transferring from 100% down constantly to zero %, so we should go each quantity in between, which means in some unspecified time in the future we’re at precisely 50 % (calculus followers would possibly acknowledge this because the intermediate worth theorem).

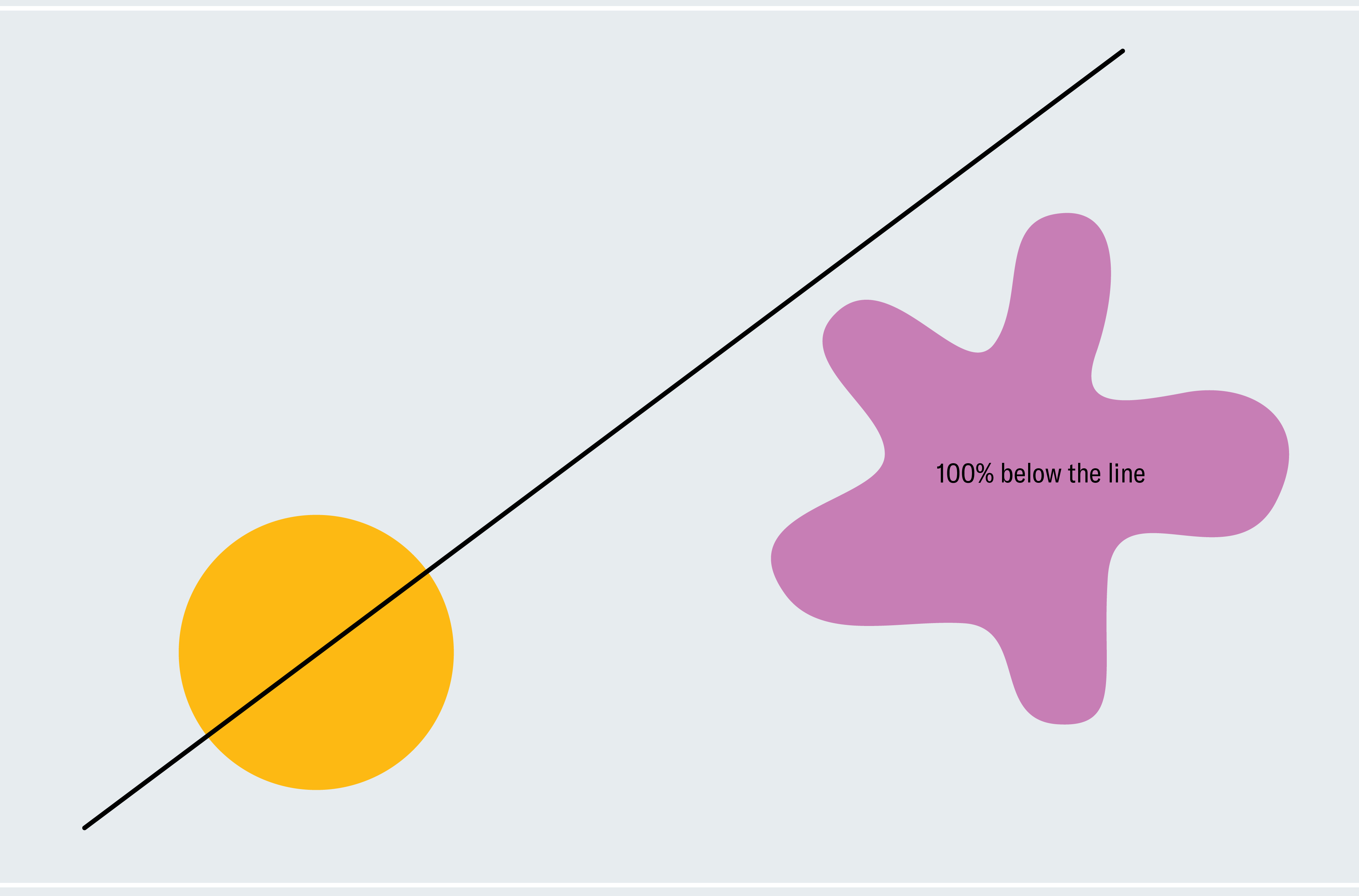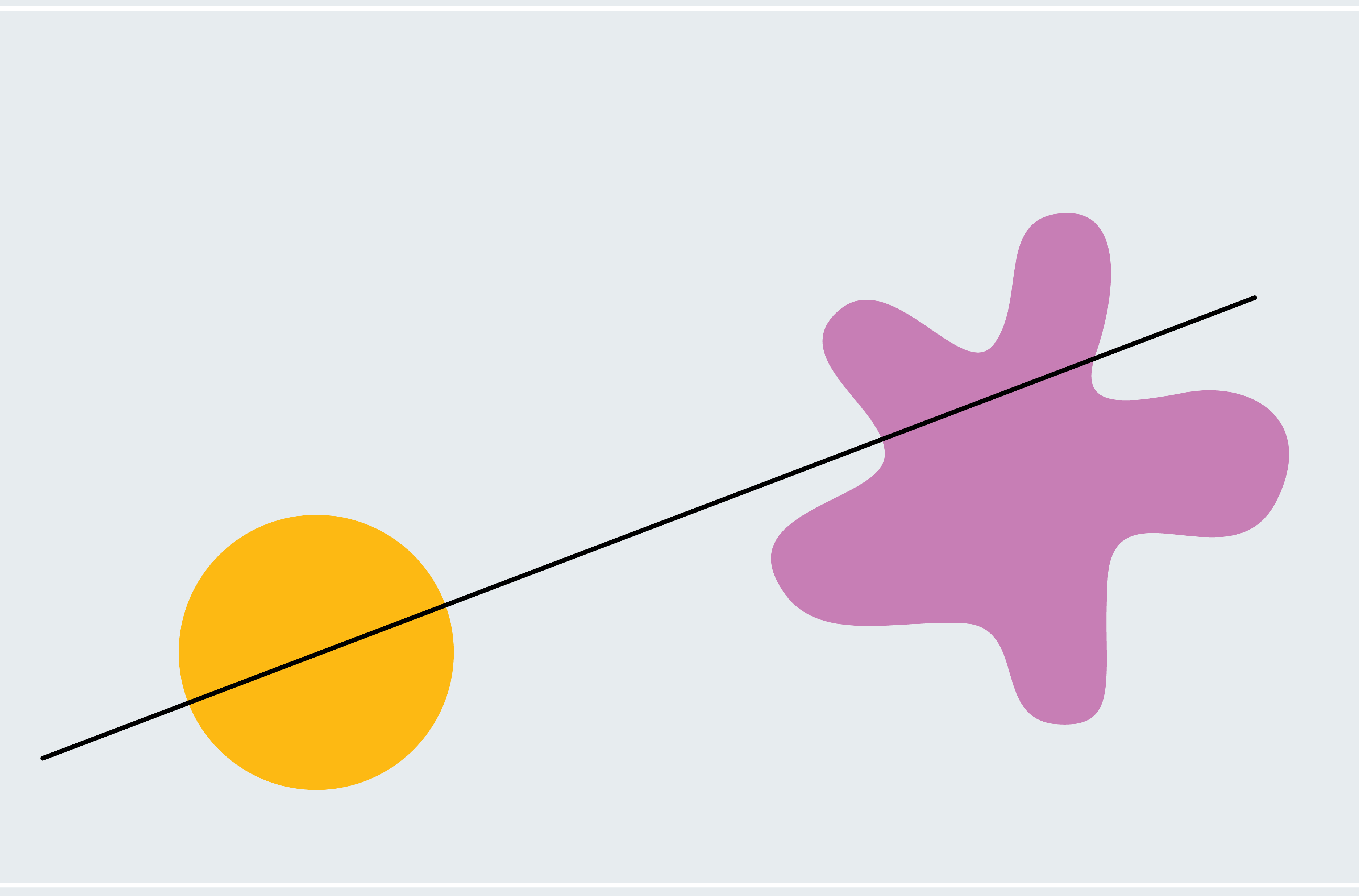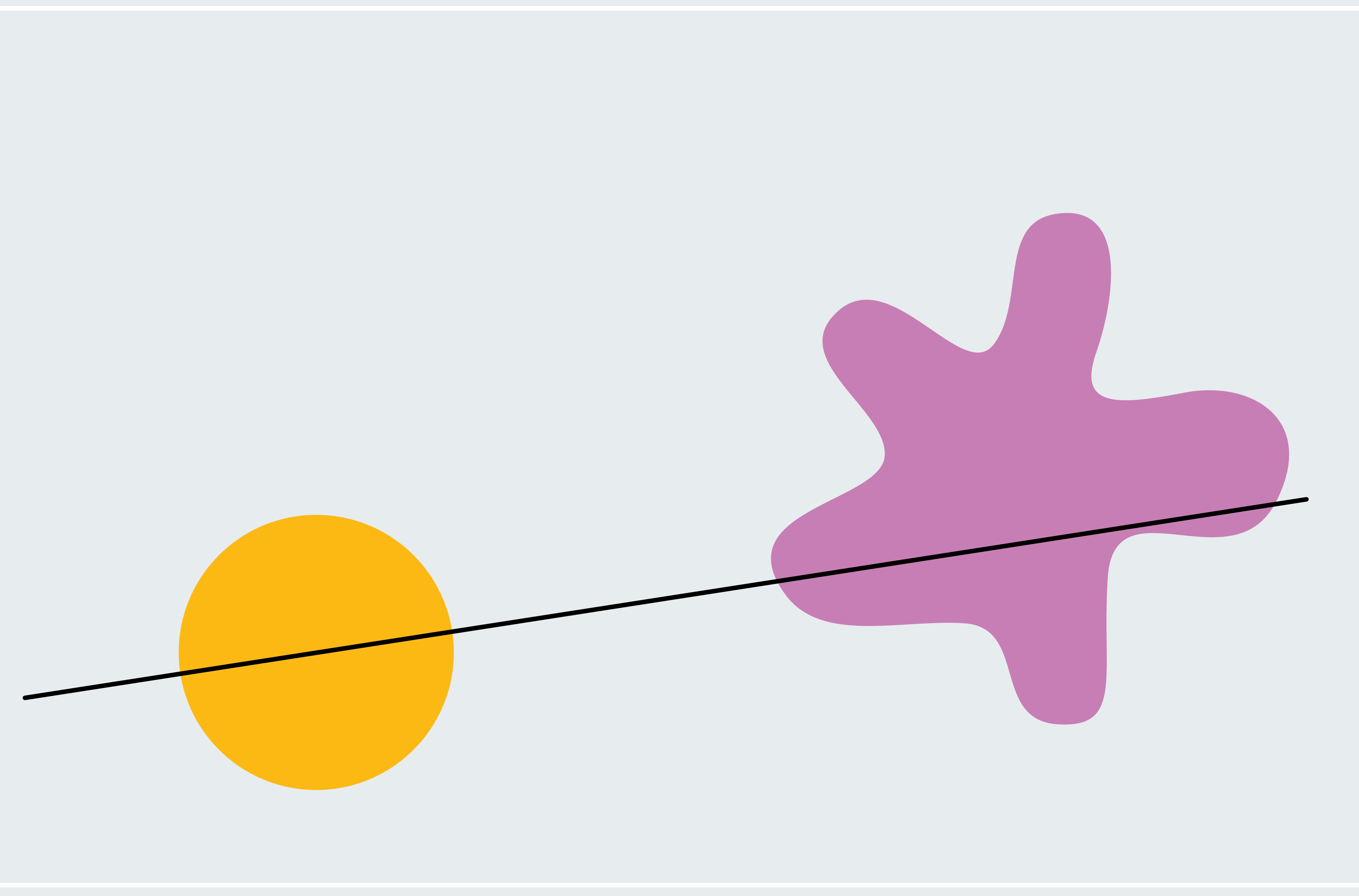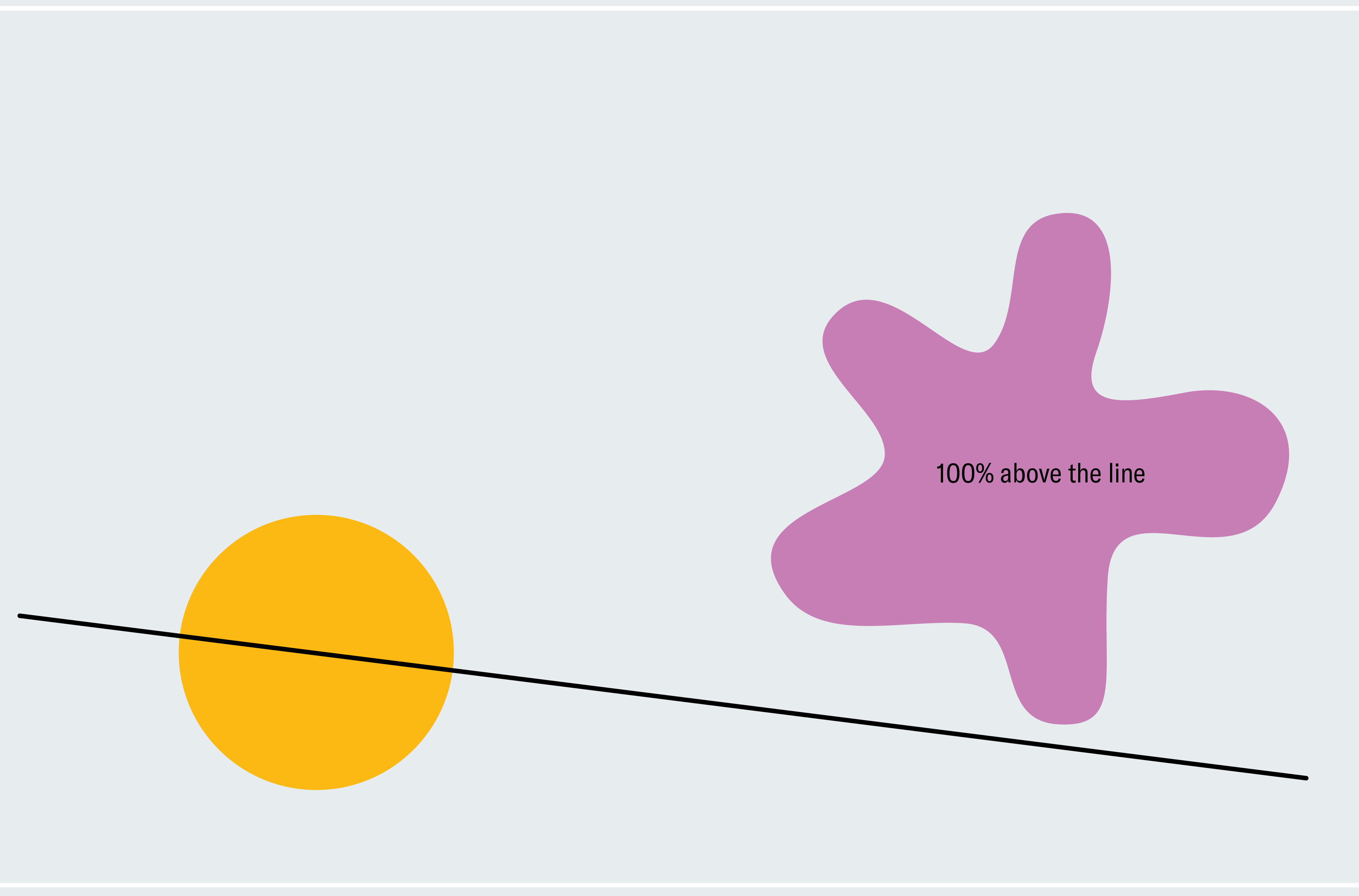
This argument proves that there’s some line that concurrently bisects our shapes (though it doesn’t inform us the place that line is). It depends on the handy truth that each line by way of the middle of a circle bisects it, so we might freely rotate our line and concentrate on the blob with out worrying about neglecting the circle. Two uneven shapes require a subtler model of our windmill approach, and the extension to a few dimensions entails extra refined arguments.

Apparently the concept holds true even when the ham and bread are damaged into a number of items. Use a cookie cutter to punch out ham snowmen, and bake your bread into croutons; a superbly equal lower will all the time exist (every snowman or crouton received’t essentially be halved, however the whole quantity of ham and bread might be). Taking this concept to its excessive, we will make the same declare about factors. Scatter your paper with pink and inexperienced dots, and there’ll all the time be a straight line with precisely half of the reds and half of the greens on both aspect of it. This model requires a small technicality: factors that lie precisely on the dividing line could be counted on both aspect or not counted in any respect (for instance, you probably have an odd variety of reds then you can by no means cut up them evenly with out this caveat).

Ponder the weird implications right here. You may draw a line throughout the U.S. in order that precisely half of the nation’s skunks and half of its Twix bars lie above the road. Though skunks and Twix bars will not be really single factors, they could as properly be when in comparison with the huge canvas of American landmass. Kicking issues up a dimension, you may draw a circle on Earth (slicing by way of a globe leaves a round cross part) that incorporates half of the world’s rocks, half of its paper, and half of its scissors, or another zany classes you want.

As talked about, the ham sandwich theorem carries far much less whimsical penalties for the perennial drawback of gerrymandering in politics. Within the U.S., state governments divide their states into electoral districts, and every district elects a member to the Home of Representatives. Gerrymandering is the observe of carving out these district boundaries intentionally for political achieve. For a simplified instance, think about a state with a inhabitants of 80 folks. 75 % of them (60 folks) favor the purple social gathering, and 25 % (20 folks) want the yellow social gathering. The state might be divided into 4 districts of 20 folks every. It appears honest that three of these districts (75 %) ought to go to purple and the opposite one ought to go to yellow in order that the state’s illustration in Congress accords with the preferences of the inhabitants. Nevertheless, a artful cartographer might squiggle district boundaries in such a means that every district incorporates 15 purple-voters and 5 yellow-voters. This manner, purple would maintain a majority in each district and 100% of the state’s illustration would come from the purple social gathering quite than 75 %. Actually, with sufficiently many citizens, any proportion edge that one social gathering has over one other (say 50.01 % purple vs. 49.99 % yellow) could be exploited to win each district; simply make it so 50.01 % of each district helps the bulk social gathering.

After all these districts look extremely synthetic. A seemingly apparent method to curtail gerrymandering can be to position restrictions on the shapes of the districts and disallow the tentacled monstrosities that we frequently see on American electoral maps. Certainly many states impose guidelines like this. Whereas it’d seem to be mandating districts to have “regular” shapes would go a great distance in ameliorating the issue, intelligent researchers have utilized a sure geometric theorem to point out how that’s a bunch of baloney. Let’s revisit our instance: 80 voters comprising 60 purple-supporters and 20 yellow-supporters. The ham sandwich theorem tells us that regardless of how they’re distributed, we will draw a straight line with precisely half of the purple voters and half of the yellow voters on both aspect (30 purple and 10 yellow on each side). Now deal with either side of the lower as its personal ham sandwich drawback, splitting every half with their very own straight line so that each ensuing area incorporates 15 purples and 5 yellows. Purple now has the identical gerrymandered benefit as earlier than (they win each district), however the ensuing areas are all easy with straight-line boundaries!

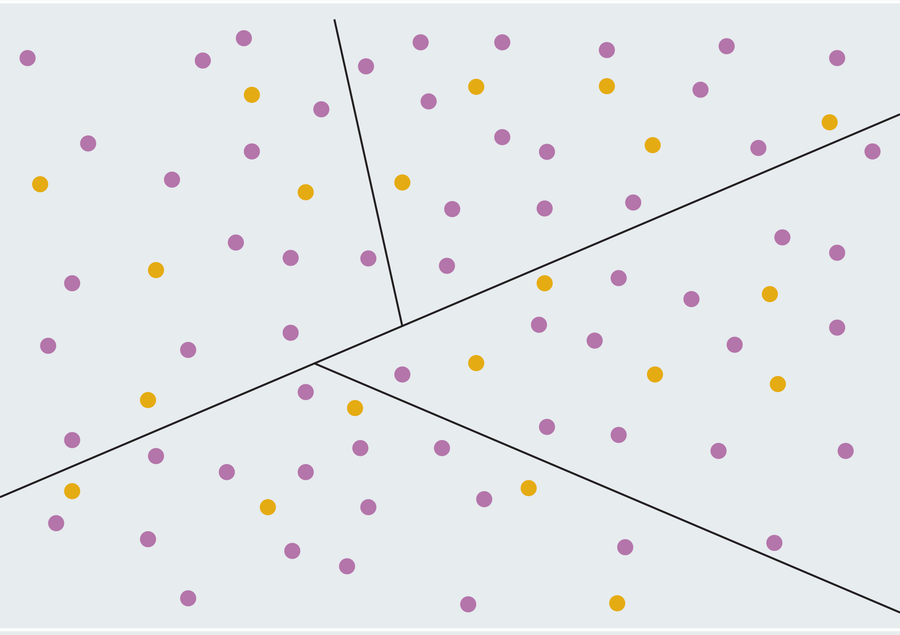
Repeated ham sandwich subdivision will all the time produce comparatively easy districts (in math-speak they’re convex polygons besides the place they doubtlessly share a boundary with an present state border). Because of this fundamental laws on the shapes of congressional districts in all probability can’t preclude even the worst cases of gerrymandering. Though math and politics could seem to be distant fields, an idle geometric diversion taught us that essentially the most natural-sounding resolution to gerrymandering doesn’t lower the mustard.